【奧數揭秘】奧數可鍛煉統籌規劃能力
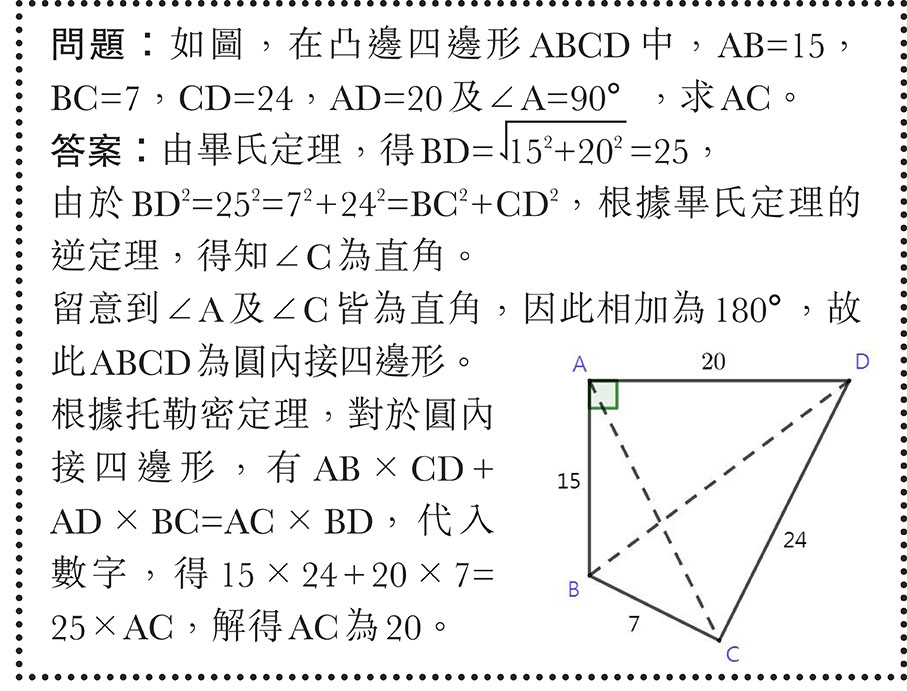
題解裏先畫圖連結對角線,在畢氏定理與其逆定理中,發現該圖為圓內接四邊形,然後用托勒密定理找到四邊與對角線的長度關係,從而找到AC。
上邊談起的托勒密定理,是課內數學沒有的定理,在競賽數學裏就會見到,通常都是作為預備知識一部分。表達形式上,除了是對於圓內接四邊形,有相關算式(即兩組對邊之積相加,為兩對角線之積)以外,還有個更普遍的形式,就是對於不是圓內接四邊形,左方大於右方,相關證明在網上很易找到,有興趣的讀者可以找找看。
在奧數裏,除了訓練學生用課內知識解難以外,也有些要另外學的定理,看幾本中學奧數書和例題,也大都能了解。早年有些奧數試題集會羅列出奧數裏常見的定理,大概都是兩頁左右,其實不多。奧數的知識範圍,總歸是無法太大的,要是涉及的基礎知識太廣闊,學生難以訓練用已有知識解難。
許多奧數的訓練,都是在一些較陌生的題目裏,常見思路無法解決之下,回顧過去經驗,找尋新線索和思考方向,然後重新組織過去知識找出解題方法。這訓練有個限制,就是預設問題本身必然是可依靠重新組織舊知識就可以解決的。
對於一般的問題,要是沒經過特殊的設計,思考起來往往難以分辨,究竟是靠全新組織舊有知識就能解決,還是需要學習新知識的,這是解決問題一般的難點。奧數的訓練,是偏向要學生發現,舊知識經過重新組織後,仍有新收穫。這些限制對於學生來說,能提供許多心得體會,有時人們習慣用舊經驗來解決問題,次數多了之後往往會假設一些新問題,仍能用舊方法解決,這也是一種認知偏差。
學會透過重新組織舊知識,比如一些定義與定理,去解決一些問題,這樣的思維得到強化訓練後,也能運用到生活中,將手上有的各樣能力、知識、資訊和資源運用起來,組織多種多樣可行的計劃,從而完成各樣自己的目標。
解難的概念,本身就滲透在各個學科或事理中,不過在這之中,數學解難的訓練成本是非常低的,可以先在腦中預想,看見自己的思想習慣或漏洞,然後再在實踐時整合資源、執行計劃,是損失比較少的學習方式。
數學本身是能訓練精思的能力,在解難中了解自己的思想限制和強項,加強思考的嚴謹度,那樣做預算和規劃時就多了成事的根據,處事才能運籌帷幄,而無須事事後知後覺,只能勉強累積一點點經驗。
● 張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
