【奧數揭秘】解題雖有捷徑 數學仍需深思

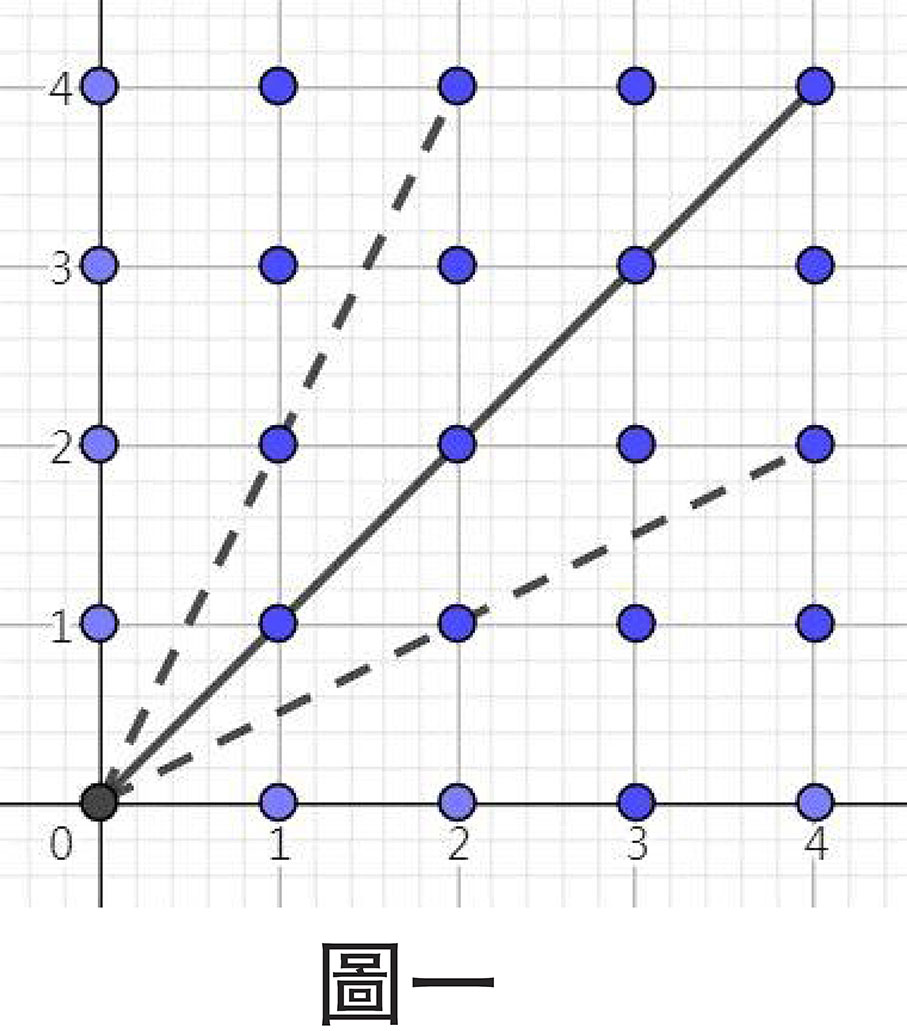
歸納一下做題思路,簡而言之,除原點以外,在範圍內任意選取兩點,然後去除跟原點共線的情況。較明顯共線的情況是在坐標軸上和實線上,在虛線的情況就較容易被忽略。
這題目其實也就是格點題型的延伸,由在原點看其他格點時,有多少格點沒被前方的格點遮擋的問題演變出來的。有兩點跟原點共線的情況,也就是有一點在另一點之後,在原點看過去,就有遮擋的情況。
競賽題裏有的題目就是一些著名問題的特例再加添變化而來,希望學生探索之中推想到更深遠的情況,比如上邊的問題裏,把可選取的正整數增加,由最大為4,改成10,以至普遍情況n,就可以問一問通項如何用n表達的問題。相關的數大了,用圖來畫線探索,可能太複雜了,可以換成格點坐標的整數性質來考慮,比如是兩個格點是否互質的問題。
有時發現,在數字小的情況下,討論的重點可能就不一樣了,比如無法用直觀的列舉做出答案,又要引入新的思想角度,要有一定的抽象思維才行。
競賽題出這些著名問題的特例,也是希望學生本身不只滿足於完成問題,要有自行推廣和探索的意願才行,只想競賽時拿高分的,可能就少了探索的動力。事實上,競賽有計分的部分,也就難免有學生把目光放在分數上,忽略了探索的重要性。
競賽題引起學習數學的興趣之後,也要學生自己在探索之中找到發展的方向才行。比如看到題目有時數字設計得精巧,省略了許多繁複的計算,但仍要仔細思索普遍情況,即使思索起來有麻煩。
做競賽題多了,也要留意解題思路上的局限,就是題目很有可能有簡潔的解法,但若考慮普遍情況,就未必時刻有簡潔的解法,正如生活裏面對的各樣問題,也未必時刻有個簡潔優雅的解決方法一樣。
看到競賽題的好處,也要明白它的限制,才能夠較全面看到它的價值。感受到競賽題簡潔美感的同時,也要了解,大多數時候數學其實是複雜的。對數學的期望合理一些,不能因為在競賽題有解題的捷徑,就認為數學總有許多捷徑,這樣學習起來心態會更好。
◆ 張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
