【奧數揭秘】掌握已知線索 推理得出答案
問題:設f(x)=(x-3)²-1,求滿足f(∣x∣)=∣f(x)∣的實數x的範圍。
答案:已知f(x)為一元二次方程,考慮圖像為拋物線,頂點為(3,-1),開口向上。考慮
f(x)=0,得x-3=±1,得x截距為4或2。
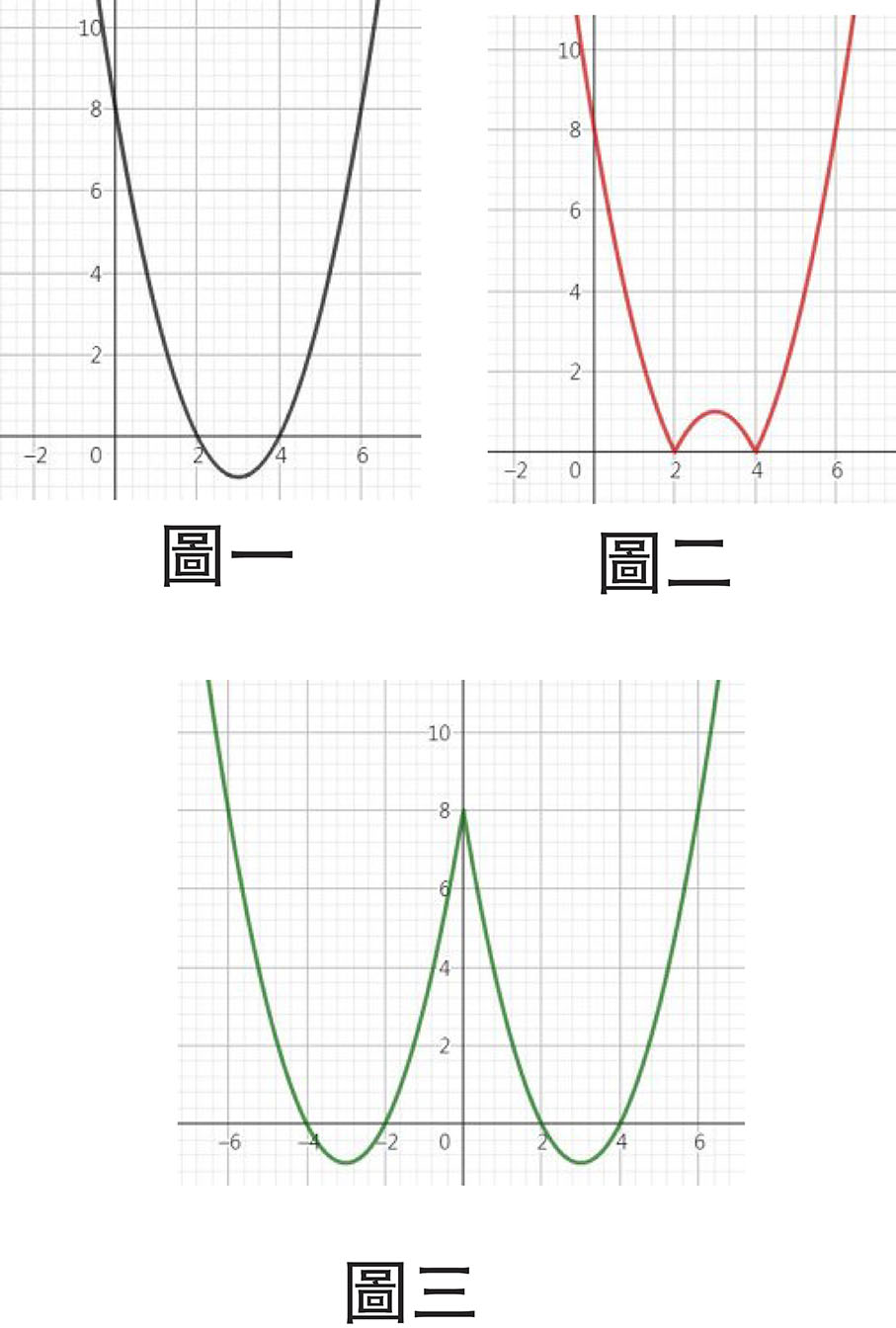
f(x)的圖像為圖一,是平常的拋物線圖像。
∣f(x)∣的圖像為圖二,則是把圖一的y值小於0的部分,沿x軸反射。
f(∣x∣)的圖像為圖三,即是把圖一裏保留x大於0的部分,再沿y軸反射。
從圖像可得知,圖二和圖三重複的部分,也就是0≤x≤2或x≥4的部分。
題解中涉及函數圖像,用上繪圖軟件來說明後就容易知道範圍。若是沒繪圖軟件,就需要對包含絕對值的函數圖像有足夠的了解才行。
大致來說,包含絕對值的圖像,相對於原本未包含絕對值的情況而言,更需要留意絕對值符號內代數式變成負數的情況。比如上邊題目裏的等式,左方若x為0或正實數時,在圖三會見到,跟圖一是一樣的,分別都在x為負數的部分。而等式右方,若分f(x)為0或正實數時,圖一和圖二的相應部分是一樣的,分別都在f(x)為負數的部分。
上邊等式左方的f(∣x∣)(圖三)中,y軸右方的圖像跟原本f(x)(圖一)一樣,那怎樣想到左方的圖像是怎樣?未有繪圖軟件,對圖像未太熟悉的時候,可以先找幾點做個對應,然後才歸納出整體情況。例如知道f(3)=-1,由絕對值的特質,也易知f(∣-3∣)=-1,那就找到其中一點。然後反覆代入幾個易計算的整數點,比如x為1、2、4等等,相應有-1、-2、-4,也會出同一個y值,也就容易說服得了自己,那個圖像是左右對稱。
而等式右方的∣f(x)∣(圖二),除了f(x)本身就大於或等於0的部分,那些f(x)變成負數的,也就另外考慮。比如考慮頂點f(3)=1,得知∣f(3)=1∣,那就發覺有些數值位置有分別,可以多取幾點看看。由於圖像是連續的,用筆畫起來時,也就易看出趨勢變化,發現圖像在x軸以下的部分,會反射到x軸上方去。
面對絕對值或者其他陌生的函數,先考慮跟原本較熟悉的函數,有什麼共通處,然後再差異處理,仔細代入數值,再由圖像連續的性質,看看圖像初步的輪廓,多少能掌握這個新的圖像。
絕對值的部分,課內也有涉及,只是談到圖像以至圖像的變換和比較較少。在圖像的變換來說,課內談起左右平移,或沿着x軸或y軸放大縮小,也已經是不少學生的難點,若是進一步談及絕對值的圖像,大概普遍比較吃力。
學生學圖像變換時往往會為了記憶各樣變換背一些口訣,形成一種固定做法,於是一旦偏離了原本的知識範圍,對圖像就覺得一無所知。
事實上,圖像變換後共通的部分還是有很多的,只要仔細代入一些數值,比如什麼時候有同一個y值、同一個x值又會算出怎樣的y值,不時會找到很多線索。探索未知,可以由已知開始。
◆ 張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
